This algorithm is also on Wikipedia, but I wanted to write a slightly modified version of it, because I think a couple of steps can be made a bit clearer than on Wikipedia, at least at the time of writing this.

Images by Wikipedia user UserTwoSix.

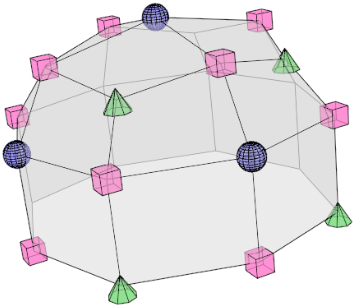
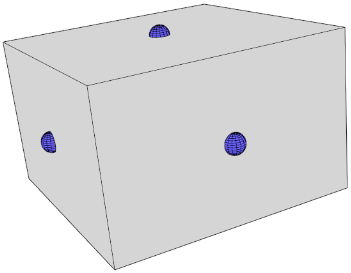
Step 1: For every face:

• Calculate the average of all its vertices

==> These are called the face points (blue spheres)

Step 2: For every edge:

• Take the average of the two vertices that the edge connects and the two face points that belong to the faces that the edge is in middle of

==> These are called the edge points (purple cubes)

• Additionally, take the average of the two vertices that the edge connects and call it the edge midpoint (not in the picture)

Step 3: For every vertex:

• Calculate F = the average of all the face points (blue spheres) of the faces that contain this vertex

• Calculate R = the average of all the edge midpoints (not in the picture) of the edges that contain this vertex

• P = the original position of the vertex

• Calculate n = the number of edges that contain this vertex

• Calculate:

(F + 2R + (n - 3)P) / n

==> These are called vertex points (green cones)

==> The new vertex positions have now been calculated. Now we just need to create the new faces.

Step 4: For every original face:

• Make new edges by connecting each face point (blue) to every edge point (purple) which belongs to an edge that the face in question contains.

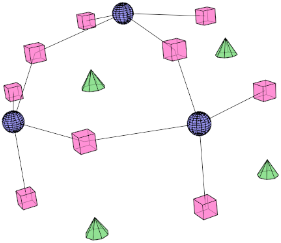
Step 5: For every original vertex:

• Connect each new vertex point (green) with a new edge to those edge points (purple) that belong to those edges that the vertex touches

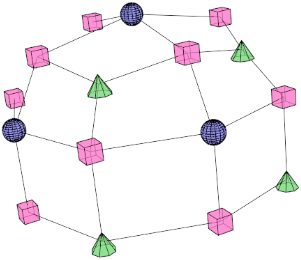
Step 6: For every new 4-vertex loop:

• New loops with four edges have formed
• Make a new face for every such loop